Resource Portal
Here you can find STEM education resources.
Search and filter below, according to your preferences, to find free activities, videos or webinars to use.
TI-Nspire CAS in Engineering Mathematics: Using Fourier Series to Find Steady-State Solution
Differential equations and Fourier series.
Publisher: T³ Europe
Author: Michel Beaudin, T³ Europe
Topic: STEM
Tags
We consider a second order linear differential equation with positive constant coefficients and a non trivial periodic input. In order to find the so-called steady-state solution, we make use of the method of undetermined coefficients using the Fourier expansion of the input. Details of computing the Fourier coefficients are given and a graph of (a partial sum of) the steady-state solution appears.
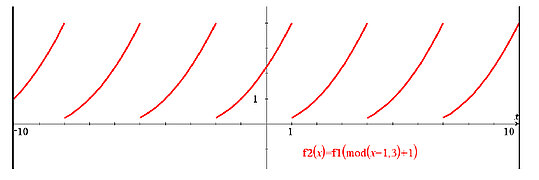
The teacher will also have the opportunity to introduce students to the modulo function of TI-Nspire CAS because it can be easily used to plot any periodic function. If f(x) is a function initially defined for a < x < b that should be extended outside the interval by periodicity of period P = b - a, then the composition f(mod(x - a, b - a) + a) will produce the expected graph. The figure below shows the parabola f1(x) = x2/4, 1 < x < 4, extended all over the line with a period 3.
This material is usually part of a differential equations course where students have also been introduced to Fourier series.